Tidal Basins#
First import some necessary packages#
import pathlib
import sys
from random import shuffle, uniform
import logging
import warnings
import IPython
import ipywidgets as widgets
import matplotlib.animation as animations
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import HTML, display
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as ipw
from matplotlib.animation import FuncAnimation
from matplotlib.ticker import MultipleLocator
import pooch
import pandas as pd
import hvplot.pandas
import panel as pn
import holoviews as hv
from PIL import Image
import coastal_dynamics as cd
pn.extension()
# # Read questions from cloud storage
questions = cd.read_questions(
"az://coastal-dynamics/questions/8_tidal_basins_hashed.json",
storage_options={"account_name": "coclico"},
)
%run initialize/init_8.ipynb
Before you is the Jupiter Notebook of week 8. This notebook consists of 4 parts:
Escoffier curve
Van de Kreeke and Robaczewska
Equilibrium concentration versus lag
Interventions
The student will practice with these topics through questions and interactive figures.
Part 1: Escoffier curve#
In chapter 9 of the Coastal Dynamics Open Textbook, we learned about tidal inlets and their stability. Tidal inlets are very dynamic and their stability depends on a lot of factors. Escoffier was the first to study the stability of tidal inlets. More specifically, he studied the cross-sectional area of tidal inlets as they change throughout the tidal cycle. From his studies, Escoffier developed the now well-known Escoffier curve. In this notebook we will use an interactive approach to better understand the Escoffier curve. Afterwards you are tasked to answer some questions to verify your knowledge on the topic.
Before starting this notebook, make sure you followed the lectures on chapter 9 (or read the slides) and read section 9.5.1 of the book.
Escoffier’s curve is a so-called closure curve and describes the relationship between maximum channel velocity \(u_e\) and the parameter \(X\), which is primarily, but not solely, a function of the channel cross-section. If we consider a sinusoidal tidal velocity signal:
Where \(\hat{u}_e\) is the tidal signal amplitude, \(P\) the tidal prism, \(A_e\) the channel cross-section and \(T\) the tidal period (see Intermezzo 9.4 of the book, equation 9.5).
The process that leads to the Escoffier curve is explained in the book. In this notebook we provide a short visualisation, see the interactive plot below. We start with an imaginary channel cross-section that is very small, close to point A, such that the tidal difference in the estuary is smaller than the tidal range. Increasing the cross-section (\(A_e\)) results in an increase of the tidal prism (\(P\)) so large that \(u_e\) increases too (recall eq. 9.5). At some point the tidal difference in the estuary is equal to the tidal range and we reach the peak of the closure curve. A larger cross-section now reduces \(u_e\) as \(P\) remains constant (again, recall eq. 9.5).
# Load the images
fp1 = pooch.retrieve("https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_1.png",
known_hash="5540ff5bda7c3c816c53068525a73cb90a90be9e612d41a21f59a11d2512128e")
fp2 = pooch.retrieve("https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_2.png",
known_hash="cc0ab29e6aebab08c15cfd82e413a99222503815000bfd62304c5c8f0925b660")
fp3 = pooch.retrieve("https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_3.png",
known_hash="97866f1e5f895b3932d625e88b614259a6d9c3016624f70ff16c9455f2cc54b9")
fp4 = pooch.retrieve("https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_4.png",
known_hash="1033c627634bee2c871196aec72d090ea80ae17612d58663c1edd327ea499ea3")
fp5 = pooch.retrieve("https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_5.png",
known_hash="b31b7799fba86c790692d97743279e2306f3f7943093e80627714fab268d82f3")
fp6 = pooch.retrieve("https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_6.png",
known_hash="31aeef48459a1d582865570a50d0b57df748a4eb8a922fbc6048d5ac4938d8c5")
fp7 = pooch.retrieve("https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_7.png",
known_hash="bcce2ca9e2cf99cbd3ca5c3e407399c80b0b6a2ecbc1a647e73390765029c7e2")
images = [
Image.open(fp1),
Image.open(fp2),
Image.open(fp3),
Image.open(fp4),
Image.open(fp5),
Image.open(fp6),
Image.open(fp7),
]
# Create the slider widget
slider = widgets.IntSlider(min=0, max=len(images)-1, step=1, value=0)
# Display the current image
image_widget = widgets.Image(value=images[slider.value]._repr_png_(), format='png', width='95%')
# Define the update function
def update_image(change):
image_widget.value = images[change.new]._repr_png_()
# Attach the update function to the slider
slider.observe(update_image, names='value')
# Display the widgets
display(slider)
display(image_widget)
Downloading data from 'https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_1.png' to file '/home/runner/.cache/pooch/3ae1eb99366e6bdc3c777d158e4b6bff-8_Escoffier_interactive_1.png'.
Downloading data from 'https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_2.png' to file '/home/runner/.cache/pooch/bdba600bd53cfc48cf91122831314c22-8_Escoffier_interactive_2.png'.
Downloading data from 'https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_3.png' to file '/home/runner/.cache/pooch/06deabd7e446d3b144baf1f4429f796b-8_Escoffier_interactive_3.png'.
Downloading data from 'https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_4.png' to file '/home/runner/.cache/pooch/48d03e9c9bc8e58a7a88fa8e9d45f56a-8_Escoffier_interactive_4.png'.
Downloading data from 'https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_5.png' to file '/home/runner/.cache/pooch/20a3624a7a85a54d049aba6cfc468e6d-8_Escoffier_interactive_5.png'.
Downloading data from 'https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_6.png' to file '/home/runner/.cache/pooch/1c43066adbff901fbb5b72117b41b344-8_Escoffier_interactive_6.png'.
Downloading data from 'https://coclico.blob.core.windows.net/coastal-dynamics/8_tidal_basins/8_Escoffier_interactive_7.png' to file '/home/runner/.cache/pooch/b39e605f6fc7de071fe384d495c7dba1-8_Escoffier_interactive_7.png'.
The next step is to determine an equilibrium channel velocity \(u_{eq}\) below which no erosion of the channel occurs. This velocity is only slightly dependent on the cross-section and can be approximated as just a function of sediment size. Larger sediment size leads to a larger \(u_{eq}\) and vice versa. The closure curve and a value for \(u_{eq}\) leads to the well-known Escoffier curve as depicted in Figure 9.22 in the book, as depicted below:
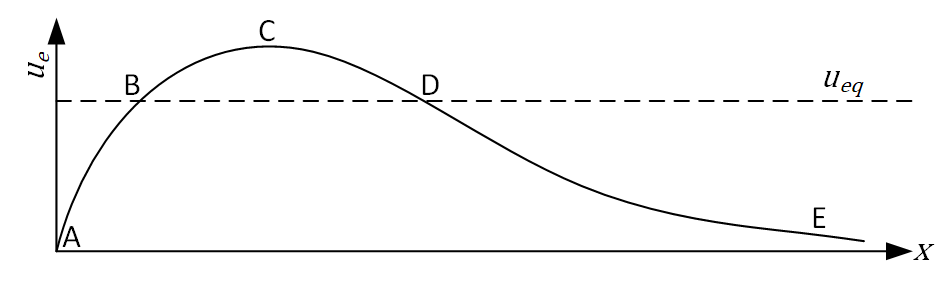
Questions#
Now that you know how an Escoffier curve is created and some of the physical processes behind it, it’s time to test your understanding. Try to answer the questions below and give your answers in the corresponding codeblock.
Channel stability#
Consider the Escoffier curve below with points A, B, C, D and E. What happens to the channel cross-section (\(X\)) at locations 1, 2, 3, 4 and 5? Where does it move to, point A, B, C, D, E or neither (N)? Give your answers below and run the codeblock to validate your answers and view your feedback.
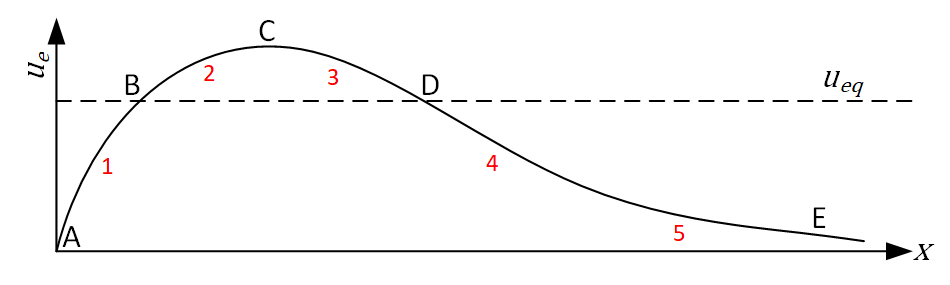
q1 = cd.QuestionFactory(questions["Q8-1"]).serve()
q2 = cd.QuestionFactory(questions["Q8-2"]).serve()
q3 = cd.QuestionFactory(questions["Q8-3"]).serve()
q4 = cd.QuestionFactory(questions["Q8-4"]).serve()
q5 = cd.QuestionFactory(questions["Q8-5"]).serve()
pn.Column(q1, q2, q3, q4, q5)
Escoffier curve “types”#
Below three Escoffier curves are shown. So far we have only considered the scenario where Point C lies above \(u_{eq}\) (scenario I). However, two other scenarios can also exist: II where point C coincides with \(u_{eq}\) and III where point C is below \(u_{eq}\). Similar to the previous question, what happens now at locations 1, 2, and 3 for scenarios II and III?

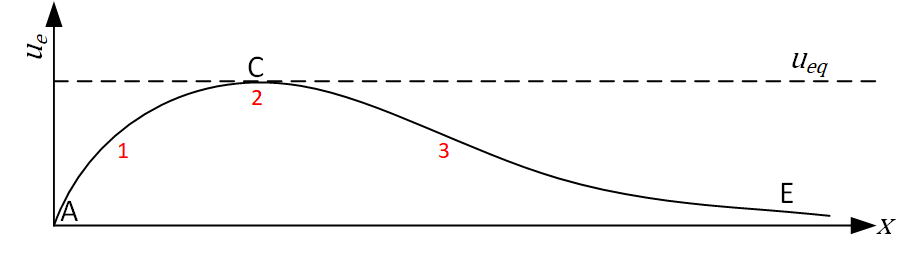
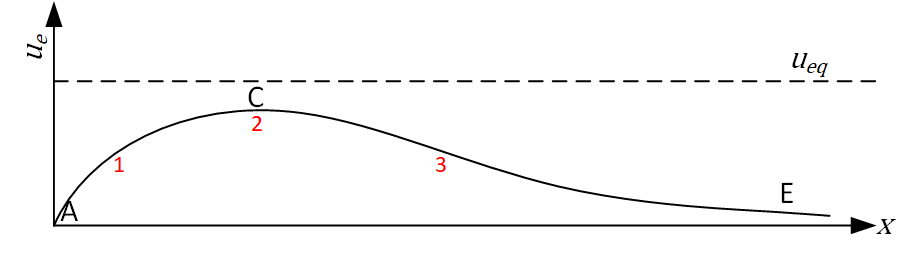
Answer the questions below.
q6 = cd.QuestionFactory(questions["Q8-6"]).serve()
q7 = cd.QuestionFactory(questions["Q8-7"]).serve()
q8 = cd.QuestionFactory(questions["Q8-8"]).serve()
q9 = cd.QuestionFactory(questions["Q8-9"]).serve()
q10 = cd.QuestionFactory(questions["Q8-10"]).serve()
q11 = cd.QuestionFactory(questions["Q8-11"]).serve()
pn.Column(q6, q7, q8, q9, q10, q11)
Changes to the Escoffier curve#
So far we have considered the typical Escoffier curve and asked you some questions on what happens with the tidal inlet. You have mastered working with the Escoffier curve, but are you also able to answer the questions below?
q12 = cd.QuestionFactory(questions["Q8-12"]).serve()
q13 = cd.QuestionFactory(questions["Q8-13"]).serve()
pn.Column(q12, q13)
Part 2: Van de Kreeke and Robaczewska#
In this section, we dive deeper into tide-induced residual transport of medium to coarse sediment using the equations derived by Van de Kreeke and Robaczewska (1993). We predominantly focus on sediment moving as bedload transport, since considering sediment travelling in suspension introduced other complications, as we shall see later.
Let us now consider how these velocity signals vary in time, and what that means for sediment transport. A velocity plot is generated by running the cell below. Flood velocities are positive.
slider_u();
<function __main__.plot_u(u0, um2, um4, um6, phi42, phi62)>
Using this figure, try to answer the questions.
q14 = cd.QuestionFactory(questions["Q8-14"]).serve()
q15 = cd.QuestionFactory(questions["Q8-15"]).serve()
q16 = cd.QuestionFactory(questions["Q8-16"]).serve()
q17 = cd.QuestionFactory(questions["Q8-17"]).serve()
pn.Column(q14, q15, q16, q17)
It is assumed that the sediment transport depends on the third power of the velocity signal: \(S \approx c u^3 \sim u^3\). Let’s plot the third power of the velocity.
slider_u3();
<function __main__.plot_u3(u0, um2, um4, um6, phi42, phi62)>
Have a look at figures 9.28 - 9.31 in the book.
Using this plot, try to answer the questions below.
q18 = cd.QuestionFactory(questions["Q8-18"]).serve()
pn.Column(q18)
The table below contains velocity and phase data for an (imaginary) estuary.
Amplitude [cm/s] |
Phase [degrees] |
||
|---|---|---|---|
M0 |
-5 |
phi42 |
240 |
M2 |
80 |
phi62 |
200 |
M4 |
15 |
||
M6 |
25 |
Let us now consider the example of a hypothetical estuary, whose tidal components can be found in the table below. Calculate the answers to the questions below using the space provided and the van de Kreeke & Robaczewska equations from Chapter 9.7.2 of the textbook.
Calculate the total transport as a function of t. Use all harmonic components for this. Use a value of \(10^{-4}\) for the coefficient \(c\).
t = np.linspace(0, 24*3600, 250)
# CORRECT THE FORMULA FOR THE TOTAL TRANSPORT HERE
total_transport = np.zeros(t.shape)
warnings.filterwarnings("ignore")
logging.getLogger().setLevel(logging.ERROR)
plot_S(total_transport)
q19 = cd.QuestionFactory(questions["Q8-19"]).serve()
q20 = cd.QuestionFactory(questions["Q8-20"]).serve()
q21 = cd.QuestionFactory(questions["Q8-21"]).serve()
q22 = cd.QuestionFactory(questions["Q8-22"]).serve()
pn.Column(q19, q20, q21, q22)
Part 3: Equilibrium concentration versus lag#
As we mentioned in Part 2, things get a little more complicated when we consider finer sediment travelling in suspension. First, we consider the equilibrium concentration that would be reached under constant flow conditions.
The table below gives velocity amplitudes and phases of the first and second harmonic of the tide.
Amplitude [cm/s] |
Phase [degrees] |
||
|---|---|---|---|
M0 |
0 |
phi42 |
180 |
M2 |
40 |
||
M4 |
10 |
Complete the code below to plot the tidal velocities.
t = np.linspace(0, 24*3600, 250)
# CORRECT THE FORMULA FOR THE TIDAL VELOCITIES U BELOW
u = np.zeros(t.shape)
plot_u_int(u)
Use equation 9.29 to plot the equillibrium concentration. Use values of \(10^{-4}\) and \(5\) for \(\beta\) and \(n\) respectively.
beta = 10**-4
n = 5
# Correct the formula for the equillibrium concentration below
c_eq = np.zeros(t.shape)
plot_c_eq(c_eq, beta, n)
Imagine we increase the sediment size. Answer the questions below.
q23 = cd.QuestionFactory(questions["Q8-23"]).serve()
pn.Column(q23)
Because fine sediment (mud), it does not respond instantaneously to the flow conditions. We need to account for this lag in our concentration and hence sediment transport calculations
Looking at equation 9.28 in the book, we can see that the equation for the the actual concentration contains a time derivative. Therefore, in order to obtain a solution for the concentration, a discretization is required. Use the following discretization (Forward Euler) for quantity u in order to model the sediment concentration:
\(\frac{D u}{D t} \approx \frac{u_{n+1} - u_{n}}{\Delta t}\).
The timestep \(\Delta t\) is already given in the code. Use a relaxation time scale of 12000 seconds. Use your solution for the equillibrium concentration from earlier.
Complete the code below to plot the concentration as a function of time.
t = np.linspace(0, 2*24*3600, 1000)
dt = t[1]-t[0]
c = np.zeros(t.shape)
for n in range(len(c)-1):
# Add your code here
...
plot_c(c)
Reflect on the plots you created with the questions below.
q24 = cd.QuestionFactory(questions["Q8-24"]).serve()
q25 = cd.QuestionFactory(questions["Q8-25"]).serve()
q26 = cd.QuestionFactory(questions["Q8-26"]).serve()
pn.Column(q24, q25, q26)
If we remove the phase difference, i.e. \(\phi=0\), the sediment response is expected to change. Adjust the code above to reflect this. Run your code again. What happens? Compare to figure 9.32 of the textbook.
q27 = cd.QuestionFactory(questions["Q8-27"]).serve()
pn.Column(q27)
Part 4: Interventions#
Now we are going to bring together many of the concepts covered in Chapter 9 to examine how natural changes and human interventions (like closing off part of the basin with a storm surge barrier) modify the morphology of tidal basins and their surrounding coastal systems. When a change occurs, the system may shift to a new equilibrium and result in a supply or demand of sediment. That relative supply or demand will determine the impact on the rest of the coastal system.
Figure 9.35 shows the effect of two different closures on the subtidal (below MLW) volume of the channels (eq. 9.17) and the ebb-tidal delta volume (eq. 9.3) as a function of the tidal prism. The figure (without interventions) is shown also below. We are going to try to reproduce the interventions made in Figure 9.35.
The most important concept is to be able to estimate how the relative supply or demand changes as the tidal prism, channels, and ebb-tidal delta change. These components are dynamically coupled in a sediment-sharing system.
Closures#
We will first look at three different closures.
# Show figures 9.35 and 9.36.
P = np.logspace(5, 11, 100)
Cv = 65 * 10**-6
Cod = 65.7 * 10**-4
Vod = Cod * P**1.23
Vc = Cv * P**1.5
df = pd.DataFrame({"P":P/10**6, "V_od":Vod/10**6, "V_c":Vc/10**6})
plot = df.hvplot.line(x='P', y=['V_od', 'V_c'], grid=True, loglog=True, xlim=(10, 5000), ylim=(2, 5000), xlabel="P [10^6 m^3]", ylabel="V [10^6 m^3]").opts(width=600, height=600)
plot
Table 9.6 is (partly) given below for Closure 1. All variables are in \(10^6\) m\(^3\).
closure 1 |
|
|---|---|
Prism before |
600 |
Prism after |
300 |
Difference in Vc |
300 |
Note that we also need to account for the subtidal channel volume inside the area that was closed off (Vch,closure in the figure below).
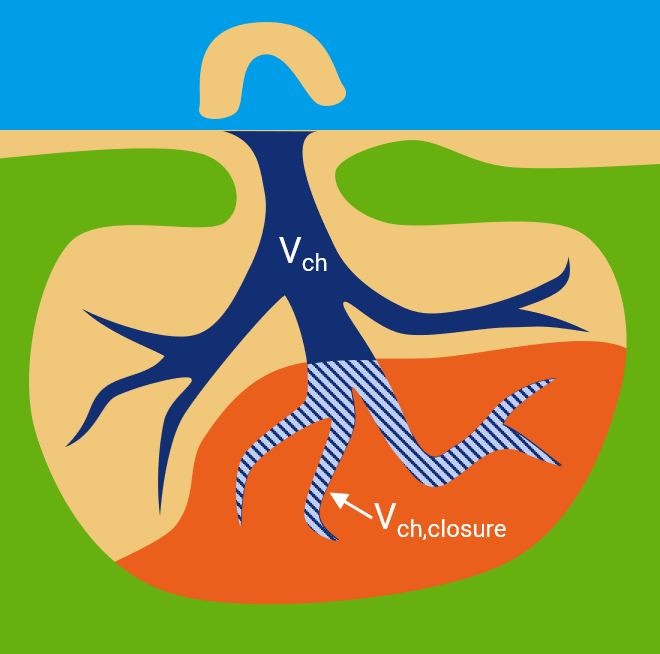 |
|
Complete the code below to calculate the \(V_{od}\) and \(V_c\) for closure 1. Also, calculate the sediment demand of the channel \(a\) and the surplus of sand in the outer delta \(b\). Use values of \(65 \times 10^{-6}\) and \(65.7 \times 10^{-4}\) for \(C_V\) and \(C_{od}\) respectively. Replace the values of \(V_{c, before}\), \(V_{c, after}\), \(V_{od, before}\), \(V_{od, after}\), \(a\), and \(b\) with the correct values and answer the questions below.
V_c_before = 0
V_c_after = 0
V_od_before = 0
V_od_after = 0
a = 0
b = 0
closure_1(V_c_before, V_od_before, V_c_after, V_od_after, a, b)
The following parameters are incorrect:
V_c_before
V_c_after
V_od_before
V_od_after
a
b
Remember to include the 10^6 in your definition of P and V!
q28 = cd.QuestionFactory(questions["Q8-28"]).serve()
q29 = cd.QuestionFactory(questions["Q8-29"]).serve()
pn.Column(q28, q29)
The code below allows you to vary axes type (linear and log-log ), plotting range, coefficients and power. Try running the cells below to replot, and test the sensitivity of these parameters and plot settings. Why do we show this as a log-log plot? What details can you see when you plot it with a linear scale? What happens when you adjust the C coefficient or power term? Which one controls the steepness and which the intercept?
# Choose between 'linear' or 'loglog' (default: 'loglog')
axes_type = 'loglog'
# Give your answer in the format [[x1, x2], [y1, y2]] (default: [[10, 5000], [2, 5000]])
range = [[10, 5000], [2, 5000]]
# Give your answer in the format [C_V, C_od] (default: [65 * 10**-6, 65.7 * 10**-4])
coefficients = [65 * 10**-6, 65.7 * 10**-4]
# Powers used for calculation of V_c and V_od respectively. (default: [1.5, 1.23])
powers = [1.5, 1.23]
P_before = 600 * 10**6
P_after = 300 * 10**6
dV_c = 300 * 10**6
plot, __, __, __, __, __, __ = plot_fig935(P_before, P_after, dV_c, axes_type=axes_type, range=range, coefficients=coefficients, powers=powers, title='')
plot
Now let’s connect this to the underlying physical concepts.
q30 = cd.QuestionFactory(questions["Q8-30"]).serve()
q31 = cd.QuestionFactory(questions["Q8-31"]).serve()
pn.Column(q30, q31)
Now let’s consider Closure 2 from the book (Figure 9.35b). The required values are given in the table below. Again, recreate the figure using the values from the table by completing the code below.
closure 2 |
|
|---|---|
Prism before |
600 |
Prism after |
300 |
Difference in Vc |
470 |
V_c_before = 0
V_c_after = 0
V_od_before = 0
V_od_after = 0
a = 0
b = 0
closure_2(V_c_before, V_od_before, V_c_after, V_od_after, a, b)
The following parameters are incorrect:
V_c_before
V_c_after
V_od_before
V_od_after
a
b
Remember to include the 10^6 in your definition of P and V!
Using the plots generated above, answer the following reflective questions.
q32 = cd.QuestionFactory(questions["Q8-32"]).serve()
q33 = cd.QuestionFactory(questions["Q8-33"]).serve()
q34 = cd.QuestionFactory(questions["Q8-34"]).serve()
q35 = cd.QuestionFactory(questions["Q8-35"]).serve()
pn.Column(q32, q33, q34, q35)
Let’s consider one more closure. Use the numbers from the table below and complete the code below. Run the code to generate a figure.
closure 3 |
|
|---|---|
Prism before |
600 |
Prism after |
300 |
Difference in Vc |
300 |
V_c_before = 0
V_c_after = 0
V_od_before = 0
V_od_after = 0
a = 0
b = 0
closure_3(V_c_before, V_od_before, V_c_after, V_od_after, a, b)
The following parameters are incorrect:
V_c_before
V_c_after
V_od_before
V_od_after
a
b
Remember to include the 10^6 in your definition of P and V!
We have seen three closures now. Did you get correct values for \(V_{c, before}\), \(V_{c, after}\), \(V_{od, before}\), \(V_{od, after}\), \(a\), and \(b\)?
Land reclamation#
Now let us consider a land reclamation. The table below provides the required numbers. Finish the code below to produce a figure.
accretion |
|
|---|---|
Prism before |
500 |
Prism after |
250 |
Difference in Vc |
0 |
V_c_before = 0
V_c_after = 0
V_od_before = 0
V_od_after = 0
a = 0
b = 0
land_reclamation(V_c_before, V_od_before, V_c_after, V_od_after, a, b)
The following parameters are incorrect:
V_c_before
V_c_after
V_od_before
V_od_after
a
b
Remember to include the 10^6 in your definition of P and V!
Using the generated plots, answer the questions below.
q36 = cd.QuestionFactory(questions["Q8-36"]).serve()
q37 = cd.QuestionFactory(questions["Q8-37"]).serve()
pn.Column(q36, q37)
Relative sea level rise#
Finally, let us consider relative sea level rise. Use the numbers from the table below to finish the code.
relative sea level rise |
|
|---|---|
Prism before |
750 |
Prism after |
750 |
Difference in Vc |
-200 |
V_c_before = 0
V_c_after = 0
V_od_before = 0
V_od_after = 0
a = 0
b = 0
relative_sea_level_rise(V_c_before, V_od_before, V_c_after, V_od_after, a, b)
The following parameters are incorrect:
V_c_before
V_c_after
V_od_before
V_od_after
a
Remember to include the 10^6 in your definition of P and V!
Finally, answer the question below.
q38 = cd.QuestionFactory(questions["Q8-38"]).serve()
q39 = cd.QuestionFactory(questions["Q8-39"]).serve()
pn.Column(q38, q39)
You have reached the end of this notebook.
